Astronomy in the mantles of Paracas
Emerita Bucher Fernandez

“El verdadero viaje de un descubrimiento no está en la búsqueda de nuevos países, sino en el ver con nuevos ojos.” Marcel Proust (1871 – 1922)
En este estudio he analizado un manto de la cultura Paracas como ejemplar, demostrando su complejidad estructural y numérica asociada a los ciclos astronómicos. Las investigaciones de William Burns (2010) acerca de los códices en los artes pre-colombinos guiaron mi mirada hacia los textiles originarios con un énfasis matemático, buscando la lógica del diseño, de las agrupaciones y repeticiones de sus componentes.
Tom Zuidema (2015) analizó los textiles Chuquibamba de la época Inca, examinando los múltiples calendarios precisos que están representados en ellos. Partiendo de los conclusiones de William Burns y Tom Zuidema, empecé a examinar los mantos de la cultura Paracas, encontrando un arte fascinante e impresionante que emplearon los paracas para visualizar ciclos solares, lunares y planetarios, hasta ciclos más complejos y largos como el gran ciclo Ahau y la Cuenta Larga, que se encuentran en los calendarios Mayas.
In this study I have analyzed a mantle from the Paracas Culture as a sample, demonstrating its structural and numerical complexity associated to the astronomical cycles. The research by William Burns (2010) on codices in pre-Colombian arts, guided my attention towards the original textiles with a mathematical emphasis, as I sought the design´s logics, as well as that of its components´ associations and repetitions.
Also, Tom Zuidema (2015) analyzed Chuquibamba textiles from the Incan time period, as he examined the multiple precise calendars represented in them.
Parting from the conclusions obtained by William Burns Glynn and Tom Zuidema, I started to examine the Paracas Culture´s mantles, and found a fascinating and impressive art the Paracas people used to visualize solar, lunar and planetary cycles, and even more complex and long cycles, such as the Great Cycle ‘Ahau’ and the “Long Count Calendar”, found in the Maya calendars.
Pacha, el espacio – tiempo
En la lengua quechua, el término “pacha” es traducido como “tiempo, suelo, lugar” (Gonzalez Holguín 1952 [1608]: 268), dando a entender que es un término tanto espacial como temporal. El análisis de las derivaciones de la categoría “pacha” según el diccionario de Diego Gonzalez Holguín, nos muestra su complejidad semántica:
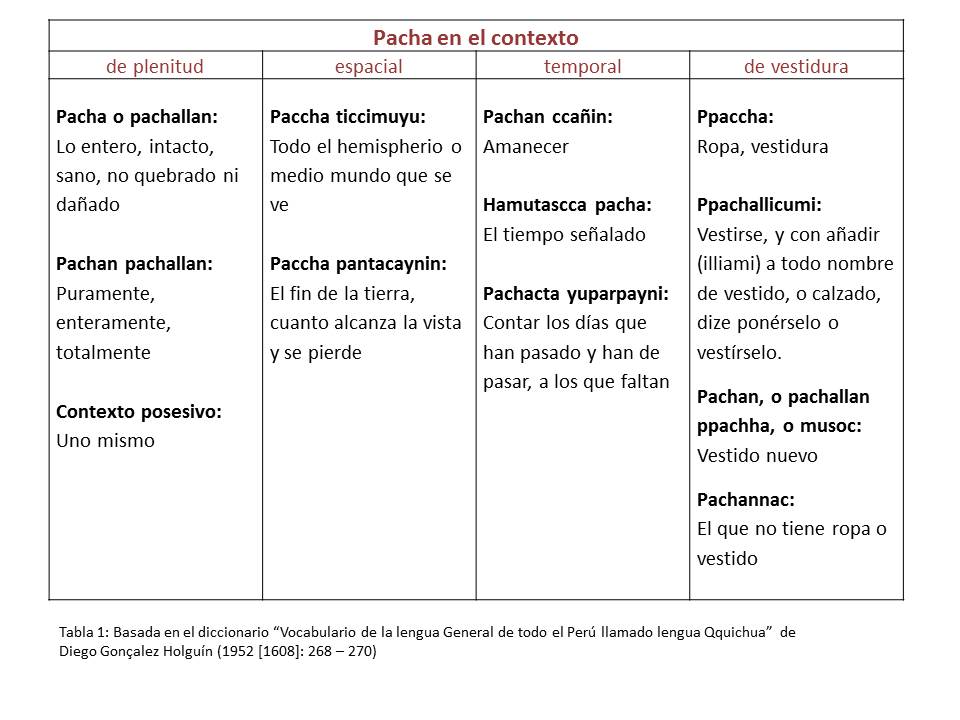
Gonҫalez Holguín (1560 – 1620) varía la ortografía de pacha, lo cual era común en esta época. En el quechua actual se pronuncia estos términos como pacha o p’acha.
Vemos que la estructura espacial siempre lo es también temporal, y es en la astrofísica donde se utiliza el término “espacio-tiempo”, que en realidad es la expresión más adecuada para el término “pacha”.
Los estudios arqueo-astronómicos realizados en el Santuario pre-hispánico de Pachacamac, situado al sur de Lima, nos muestran una astro-arquitectura precisa, donde el tiempo está integrado en el diseño espacial arquitectónico de manera inseparable:
“Pachacamac” es también un gran santuario astronómico: El territorio y los templos registran el ciclo anual del Sol y el gran ciclo de la luna (18 años), la salida de la Cruz del sur hacía Pucusana, el Inti Raymi hacía Lomo de corvina… El templo del Sol además del solsticio de verano señala la constelación de Escorpio llamada Amaru por los Incas… la gran serpiente celestial. Sus ocupantes ritualizaron el ciclo de las estaciones y los astros… armonizaron su vida con la naturaleza (Pinasco, 2013).
Partiendo del término “pacha”, se nos abre una vista fascinante hacía los textiles pre-hispánicos, en los cuales las civilizaciones andinas plasmaron el espacio con su tiempo. Estos textiles formaron parte de una mnemotécnica altamente desarrollada, aplicando un arte científico de visualizar los períodos temporales-espaciales. Observar sus textiles, es acceder a un conocimiento visualmente, donde la matemática es introducida de manera artística y estética, donde el cálculo es movimiento, ritmo, diseño y color.
En mis análisis de los textiles paracas he aplicado la numerología del calendario Maya, lo que resultó exitoso y afirma la conclusión de Wiliam Burns en su análisis de una clavina paracas: “Fijaron un calendario de 360 días y conocieron también un período de 260 días recuerda al Año Sagrado o Año Mágico de los Zapotecas y los Mayas” (Burns 2010: 316).
Entendí que la numerología Maya es la base de una metodología para encontrar el pulso y los ritmos del cosmos, dando paso a las celebraciones del calendario. Así, he concluido que el denominado calendario Maya no solo fue utilizado en centro-américa, sino, esta numerología fue aplicada también en el antiguo Perú, tal como vamos a ver con el análisis de este textil de Paracas, que expongo como un ejemplar de un sistema matemático-astronómico, lo cual, según mis análisis, es aplicable para la mayoría o quizás para todos los mantos de la cultura paracas.
El manto expuesto es de la fase Paracas Necrópolis (ver fig. 1).Es un tejido llano de urdimbre y trama discontinua, anillado cruzado y bordado en estilo Bloque de color, hecho de fibra de camélido. Tiene una extensión de 252 x 109 cm. (Museo Chileno de Arte Precolombino 2015: 83).
Esta relación de tamaño que se representa en este textil es muy interesante, porque coincide exactamente con la relación geométrica-astronómica del espacio-tiempo solar, que consiste en la representación de los “ángulos” solsticiales que son provocados por la declinación del eje terrestre de 23.5 °:
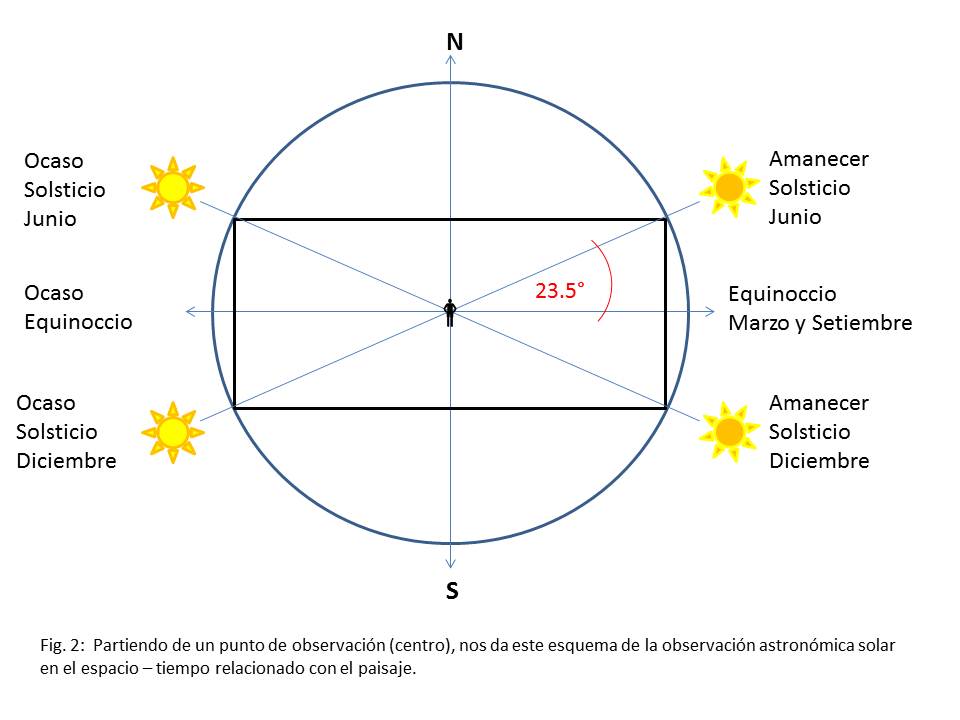
Comparamos con el manto:

Fig. 3: Manto paracas, aplicando el ángulo de 23.5°.
Retomando el término “pacha” en su contexto espacio-tiempo y de plenitud, esta forma rectangular representa esta geometría astronómica que nos da el tiempo, proyectada en el espacio, suelo, tierra, donde uno se encuentra, y al mismo tiempo, alzando la mirada hacia el movimiento de los astros, en el espacio celeste. Para integrar el tiempo en el espacio (lo denomino Astro-arquitectura), la observación del calendario paisajista (landscape calendar) surge entre los puntos solsticiales de las salidas y bajadas del sol, y son la base para la reconstrucción del pacha en el que vivimos y nos movemos.
La visualización de los cálculos astronómicos
Es fascinante, como los paracas empleaban todo una matemática astronómica en el arte textil, partiendo de esta forma rectangular básica:
Empezaremos el análisis desde el borde, llegando paso por paso al centro. Todos los mantos de Paracas tienen una estructura particular respecto a los bordes: Siempre son dos bordes que rodean un textil, sin interrupciones a los lados largos, pero pausando en el medio de los lados cortos (ver imagen N° 1)Supongo que los bordes pausados tienen que ver con los movimientos y la visibilidad de los astros, que aparecen, desaparecen y reaparecen, en un ritmo constante e infinito.
 Examinando los flecos, vemos que están estructurados en grupos de 8 colores (fig. 4): Rojo, verde, blanco, negro, marrón, violeta, ocre y azul. Esta sucesión se repite en los dos bordes. Podemos contar a un lado 154 grupos de flecos, y al otro lado 160 grupos a 8 colores. En total son 314 grupos de flecos. Son repartidos en dos bordes, pero no divididos entre dos lados iguales. Como cada grupo tiene 8 colores, podemos hacer los siguientes cálculos:
Examinando los flecos, vemos que están estructurados en grupos de 8 colores (fig. 4): Rojo, verde, blanco, negro, marrón, violeta, ocre y azul. Esta sucesión se repite en los dos bordes. Podemos contar a un lado 154 grupos de flecos, y al otro lado 160 grupos a 8 colores. En total son 314 grupos de flecos. Son repartidos en dos bordes, pero no divididos entre dos lados iguales. Como cada grupo tiene 8 colores, podemos hacer los siguientes cálculos:
154 x 8 = 1232 = 14 ciclos siderales de Mercurio, exactos. (1 ciclo sideral es de 88 días: 88 días x 14 = 1232 días)
160 X 8 = 1280 = 11 ciclos sinódicos de Mercurio, +4 días
(1 ciclo sinódico es de 116 días)
Es sorprendente que ambos cálculos están claramente vinculados con el planeta Mercurio. Mercurio es el planeta más cercano al sol, dibujando la primera órbita en el sistema solar, y observando desde la tierra, sigue al sol, por estar tan cerca de él, dejándose ver solo en raras oportunidades matutinas u ocasos. Obviamente, los flecos nos introducen a los ciclos siderales y sinódicos de Mercurio, pero lo fascinante es la distribución de dichos flecos:
Mientras que el borde superior tiene un número exacto de 14 ciclos siderales mercurianos, el borde inferior marca 11 ciclos sinódicos, con un aumento de 4 días. Sin embargo hay en este borde una parte, que siempre me deja en duda, y es la que está situado bajo la sexta figura antropomorfa contando desde el lado derecho. No tiene la secuencia común de los colores en los grupos, parece simétrico, y carece del fleco blanco. A pesar que la foto proporcionada por el Museo Chileno de Arte Precolombino tiene una alta resolución, no puedo distinguir esta irregularidad con certeza. Seria increíble, si se hubiera hecho esta corrección allí misma para alcanzar el número exacto, ya que con un múltiplo de 8 no se llega a los 11 ciclos sinódicos exactamente.
Partiendo de los 11 ciclos sinódicos de Mercurio, llegamos exactamente a 14.5 ciclos siderales de Mercurio, y a 3.5 años solares menos un día y medio:
160 x 8 = 1280 = 11 x 116 + 4
11 x 116 = 1276
1276 días = 14,5 x 88 días = 11 x 116 días = 3,5 x 365 días – 1,5 días
1276 días = 14,5 Mercurio sid. = 11 Mercurio sin. = 3,5 Años solares – 1,5 días
Duplicamos estos números, pensando que un borde es solo la mitad de una plenitud, ya que el manto está dividido en dos bordes, llegamos al siguiente ciclo expresado en números enteros:
29 Ciclos Mercurio sideral = 22 Ciclos Mercurio sinódico = 7 Años Solares – 3 días
Es muy interesante que se muestre en este borde de flecos un tiempo de 7 años solares, relacionados con los ciclos de Mercurio. Examinando la sincronización entre el ciclo sinódico de Mercurio de 116 días y su ciclo sideral de 88 días, vemos que cada 7 años solares concuerdan exactamente con un número entero, con una diferencia de 3 días enteros para ajustar a los años solares (ver Tabla 2).
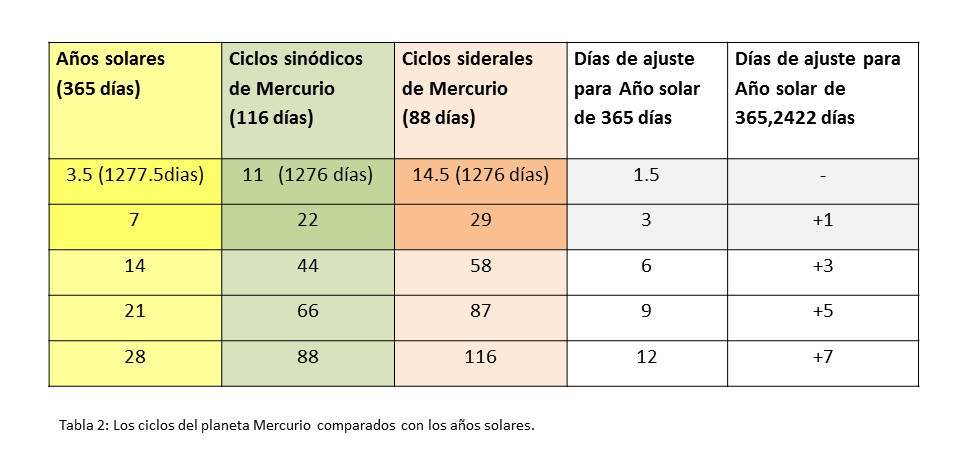
Esta tabla se puede continuar infinitamente, pero con 28 años solares hay un juego interesante con los números de los ciclos sinódicos y siderales mercurianos, ya que sus números de ciclos y sus días de los ciclos se invierten, y se reflejan el sideral y el sinódico.
Retomando el borde superior de los flecos, tenemos 154 grupos de flecos de 8 colores. También con estos números se puede realizar interesantes cálculos, pero en este caso son relacionados con los ciclos del mercurio y el calendario lunar sinódico. Un año lunar sinódico de 12 meses (un mes a 29.5 días) es 354 días. En este año lunar entran 4 ciclos siderales de mercurio (4 x 88 días = 352 días), sumando tan solo 2 días para completar al año lunar (Tabla 3). Retomamos los cálculos de los dos bordes arriba mencionados, y duplicamos también este borde:
154 x 8 = 1232 días = 14 ciclos siderales de Mercurio = 3.5 años lunares sinódicos – 7 días
154 x 8 x 2 = 2464 días = 28 ciclos siderales de Mercurio = 7 años lunares sinódicos – 14 días
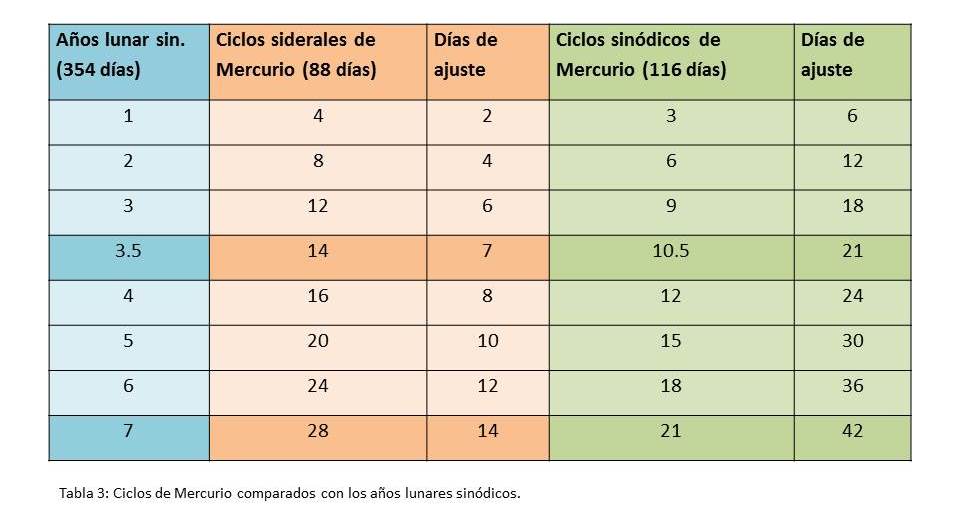
Concluyo que los flecos de un lado del borde relacionan los ciclos de mercurio con 7 años solares, mientras al otro lado, los flecos señalan los ciclos de Mercurio con 7 años lunares.
Y para concluir el tema de los flecos, otros juegos de cálculos con estos números:
11 x 14 = 154
14 años solares – 14 años lunares = 154 días
________________________________________________________________________________________

Fig.5: Detalle con un “pallar” antropomorfo y borde con aves. Imagen del Museo Chileno de Arte Precolombino, 2015: 85
A continuación de los flecos sigue un borde tejido con diminutos aves (ver fig. N° 5).
Contamos a un lado 146 unidades, y al otro lado 169, en total son 315 figuritas. Pensando que los flecos representan días, supongo que los avecitas tendrían que expresar otro número. Apoyándome en el calendario Maya, remplazo cada figurita con 20 días, que se denomina Uinal en el sistema numérico Maya:
Borde superior: 146 Uinales = 146 x 20 días = 2920 días.
Es sorprendente, que tan solo adicionando 2 días, tenemos el ciclo pentagonal de Mercurio – Tierra – Venus:
“Si eliminamos“ la excentricidad y convertimos la órbita de Mercurio en un círculo racional perfectamente equidistante del Sol, resulta que la órbita de Mercurio inscribe a un pentágono (inscrita en la órbita “perfeccionada” de Mercurio), y este pentágono es la figura interior que resulta de la estrella de 5 puntos formada por la Tierra y Venus durante 8 orbitas de la Tierra y 13 de Venus (8 años), lo cual es el ciclo Pentagonal.” (Rivas 2017)
Aquí se puede observar la secuencia que muestra los 5 ciclos sinódicos de Venus que ocurrieron durante los dos tránsitos del 2004 y del 2012:
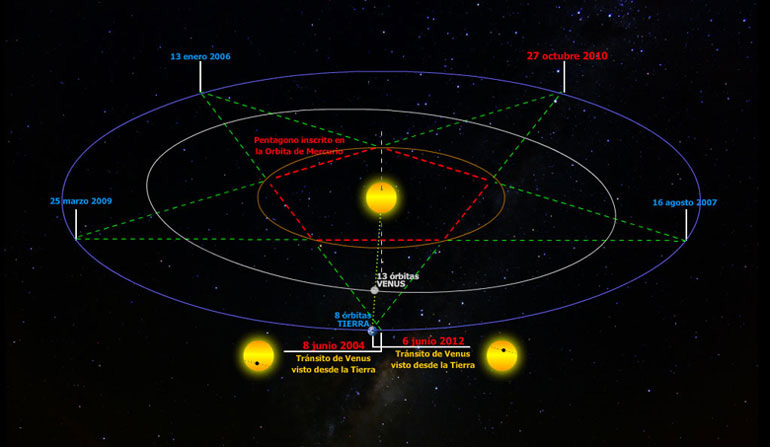
Fig. 6: Ciclo pentagonal, imagen de Rivas Pablo, 2017
La habilidad matemática que empleaba el autor o la autora de este textil para calcular con más facilidad usando números enteros es interesante y nos muestra que el número 2920 es cómodo e igualmente exacto. Comparamos los números exactos astronómicos con los números aplicados en el manto:
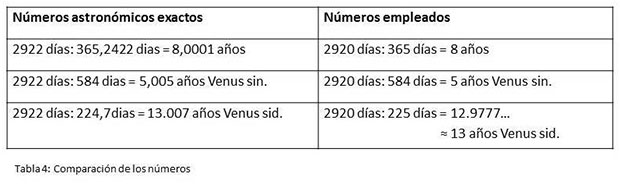
El otro borde contiene 169 figuritas:
169 Uinales = 169 x 20 días = 3380 días
3380 días : 225 días = 15.0222 ≈ 15 años Venus sid.
Sumando los dos bordes nos da el siguiente cálculo:
146 Uinales = 2920 días= 13 años Venus sid= 5 años Venus sin= 8 años Tierra= Ciclo Pentagonal
169 Uinales = 3380 días = 15 años Venus sid
____________________________________
315 Uinales = 6300 días = 28 años Venus sid = 8 años Marte sin. = 17 ¼ años Tierra = 17.5 Tunes
Estos 28 años de Venus sideral nos guían al próximo planeta, el Marte:
En 17¼años de la tierra hay 8 periodos de Marte. Vemos que en todo este borde, la guía son los ciclos siderales de Venus, para conducir a las alineaciones de ciclos mayores, como al ciclo pentagonal en un borde, y completando en el otro borde con los 15 periodos de Venus sideral, al ciclo Venus – Tierra – Marte, dando un preludio a la Cuenta Larga de 1 872 000 días, que son 5125 años:
En sincronía con el Tzolkin, la unidad cíclica mínima es 18 720 dias (= 51,25 años), en los que sincronizan 72 Tzolkines y 24 ciclos sinódicos de Marte (e incluso 52 Tunes de 360 Kines y 936 Uinales de 20 Kines). Es de observar que 18 720 días (72 Tzolkines, 24 ciclos sinodicos Marte y 52 Tunes) es la centésima parte de la Cuenta Larga. (Rivas 2017).
Lo representado en este borde con las aves son los 8 ciclos sinódicos de Marte, que es la tercera parte de los 24 ciclos marcianos, y 17 años solares terrestres que es el tercio de los 51 años. Así se nos muestra la tercera parte de la unidad cíclica mínima que es la centésima parte de la Cuenta Larga. He cuestionado porque no representaban este ciclo con 312 Uinales, sino con 315 Uinales. Resulta que si tomamos como constante el ciclo sideral de Venus, se requiere emplear el número 315. Estos números finalmente nos guían a los cálculos y números de la Cuenta Larga.
____________________________________________________________________________________
Seguimos analizando los bordes, examinando los seres antropomorfos que siguen a las avecillas (Ver fig. 5 y fig. 7). El cuerpo de estos seres me recuerdan a pallares o habas, y las figuras permiten una trampa visual al voltear la posición.

Fig.7: Detalle del manto
Dichas figuras están rodeando el textil caminando al sentido del reloj, o visto diferente, circulando naciendo en el sentido contrario del reloj, claramente están dando un movimiento circular. Podemos contar los “brotes” del “pallar” antropomorfo:

Fig.8: El pallar antropomorfo con sus apéndices y los números de “brotes”.
Estos números permiten un juego de cálculos muy interesante:
La proporción de 26 a 10 es lo mismo como la proporción del ciclo sinódico de Venus con su ciclo sideral:
26 : 10 = 2.6 / 585 : 225 = 2.6
También se puede expresar que 26 ciclos Venus sideral son igual a 10 ciclos de Venus sinódico:
26 x 225 días = 10 x 585 días
26 Venus sideral = 10 Venus sinódico
Y otro cálculo surge, si substraemos del ciclo sinódico de Venus el sideral:
585 dias – 225 dias = 360 dias. Aquí vemos la relación de los dos ciclos venusinos con los números 26 y 36, y finalmente con el ciclo Ahau:
26 x 36 = 936 = un centésimo Ahau
La magia de la matemática paracas aumenta cuando consideramos las unidades de los “pallares antropomorfos”. Cada lado contiene 16 unidades, en total hay 32 “pallares” en el manto (ver fig. N°1). Examinando los posibles cálculos, surgen los siguientes variantes:
16 x 225 días = 3600 días = 10 Tunes / 32 x 225 días = 7200 días = un Katun
16 x 585 días = 9360 días = un décimo Ahau / 32 x 585 = 18 720 días = un quinto Ahau
Un Ahau es un ciclo grande del calendario Maya de 93 600 días (≈256 años). Este ciclo une los años Tzolkin y Tun, y los ciclos de Venus y Marte:
1 AHAU = 260 Tunes = 360 Tzolkines = 160 Venus sin. = 416 Venus sid. = 120 Marte sin
Multiplicamos un Ahau con 20 recibimos la “Cuenta Larga” de 1 872 000 días, que son más de 5125 años.
Cuenta Larga =5200 Tun =7200 Tzolkin = 3200 Venus sin. =8320 Venus sid. =2400 Marte sin.
______________________________________________________________________
De esa manera llegamos al diseño escalonado que predomina en el manto (ver fig. N° 9):
Examinando los cuadrados □, podemos observar la siguiente estructura:

Vemos que los resultados predominantes son 72, 80 y 82.

Fig. 10: Detalle
Pero un cuadrado tiene una estructura dual, con 5 escalones, lo que se puede asociar con los siguientes números:
1 cuadrado
2 colores
5 escalones por color
10 escalones por cuadrado
Si tomamos la cifra 72 y jugamos con estos números, nos da los siguientes resultados:
72 x 2 = 144 / 72 : 2 = 36
72 x 5 = 360 / 72 : 5 = 14,4
Y vemos también el rol que juega el número 1 y el factor 10. Comparamos esta cifra y sus resultados con el calendario Maya:
Un Tun = 360 días
Un Katun = 20 Tun = 7200 días
Un Baktun = 20 Katun = 144 000 días
Pero con estos números dentro del “Calendario Maya” también hay las siguientes relaciones:
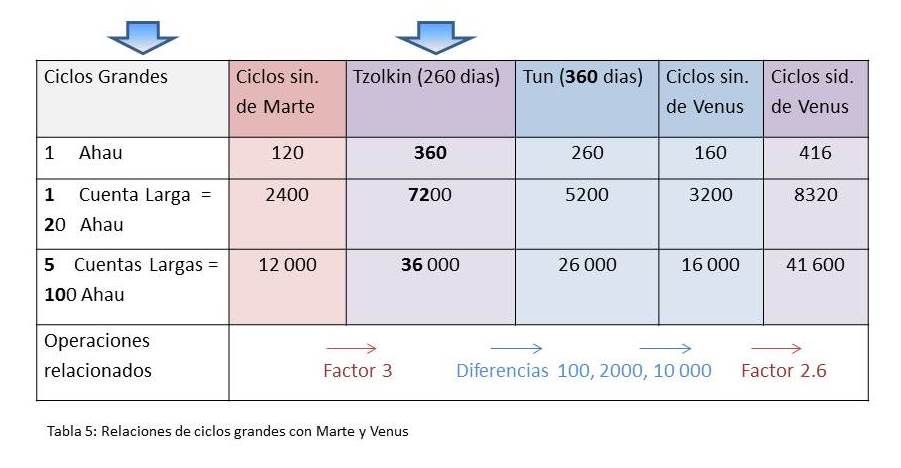
Y observando la tabla, podemos ver las relaciones de estos números con los ciclos planetarios en comparación con los Ciclos Grandes. También podemos distinguir los números de la primera fila de los Ciclos Grandes, que expresan la misma relación numérica como el “cuadrado escalonado” arriba mencionado.
Lo fascinante en este sistema numerológico y su diseño es su aplicación versátil, que permite otro juego, si remplazamos cada cuadrado escalonado con un Tzolkin:
72 x 260 días = 18720 días
72 Tzolkin = un centésimo de la Cuenta Larga = un quinto Ahau
Estos cifras nos suenan, son las mismas de la Cuenta Larga que tiene 1´872´000 días (7200 x 260).
Y si consideramos el factor 5 en este juego con el Tzolkin, llegamos exactamente a un ciclo Ahau:
72 x 5 = 360
360 x 260 días = 93’600 días
Tun x Tzolkin = Ahau
Queda resolver los números 80 y 82, que se recibe sumando los espacios entre los bordes.
El diseño escalonado he encontrado en todas las culturas pre-colombinas, es un patrón milenario, y basado en mis investigaciones he concluido, que también está relacionado con los ciclos de la luna. La luna dibuja también un rectángulo como el sol (ver fig N° 2), pero lo que el sol lo dibuja en un año, la luna lo hace en un mes, diariamente posponiendo sus salidas por 50 minutos, y cambiando su imagen con los diferentes fases. Empleando sus horas de salida dentro del pacha solar rectangular, y considerando sus fases lunares, se adquiere automáticamente este diseño escalonado.
Si relacionamos el número 80 (considerando solo los cuadrados enteros del manto) con la luna sideral, nos da los siguientes posibles cálculos:
80 x 27,3 días = 2184 días = 6 x 364 días
80 x 27⅓ días = 6 x 364 días + 11 horas = 6 Años Solares
Y tomando en cuenta los 12 meses del Año Solar, podemos ver la siguiente relación:
80 meses lunares siderales = 6 Años Solares = 72 meses solares
Propongo, que la segmentación de la agrupación de los cuadrados en el diseño interior permite la multiplicación de 6 x 12 = 72 (6 años a 12 meses son 72 meses), y con la adición de los cuadrados enteros laterales, se obtiene la comparación de los meses solares con los meses lunares en 6 Años Solares de manera visual.
Pero jugando nuevamente con los números 2, 5 y 10, podemos calcular lo siguiente:
80 x 2 = 160 80 : 2 = 40
80 x 5 = 400 80 : 5 = 16
Si se multiplica 16 con el ciclo sideral de Venus se recibe otra vez 10 Tuns:
(80: 5) x 225 días = 10 x 360 días
16 Venus sid. = 10 Tun
Seguimos jugando, incorporando el siclo sinódico de Venus, nos recuerda al juego numérico de los pallares, esta vez aplicando el factor 2 a la cifra 80:
(80 x 2) x 585 días = 93´600 días
160 Venus sin. = 1 Ciclo Ahau
(80: 2) x 585 días = 90 x 260 días = 65 x 360 días = 30 x 780 días = 23´400 días
40 Venus sin. = 90 Tzolkin = 65 Tun = 30 Marte sin = ¼ Ahau
Y si multiplico el número 40 con el Año Solar, recibo 5 ciclos pentagonales:
40 Años Solares = 65 ciclos Venus sid. = 25 ciclos Venus sin.
Queda la pregunta, si los cuadrados divididos en las esquinas son “casuales”, es decir surge por completar simplemente el diseño escalonado hasta el borde, o si tiene que ver con un ajuste a otro ciclo. Observemos:
82 días son exactamente 3 meses lunares siderales: 3 x 27⅓ = 82
Y también hay un juego de estos números con los números 2 , 5 y 10 del diseño escalonado:
82 días x 5 = 410 días = 15 x 27⅓ días = 15 meses lunares siderales 82: 5 = 16.4
82 días x 2 = 164 días = 6 meses lunares siderales 82: 2 = 41
El numero 164 corresponde al medio año lunar, dado que 328 días forman el año lunar sideral de 12 meses a 27⅓ días, y el número 41 segmenta este calendario en semanas:
“El número 41 recuerda al sistema de seques de los Incas, que representa un calendario lunar sideral y forma parte de la estructura social Inca: “En el Cuzco dos organizaciones supervisoras estaban a cargo de los rituales calendáricos, la primera de ellas en función a los “meses” y la segunda a 41 “semanas”. Podemos relacionarlas respectivamente con grupos de ceques y con ceques. Posteriormente sostendré que los meses originalmente se derivaban de un calendario solar anual (12 x 30/31 = 365) y las semanas de uno lunar sideral (41 x 8 = 12 x 27 ⅓ = 328).”(Zuidema ,2015: 40)
Y finalmente, el ciclo de la luna sideral y el número 82 tienen algo común con el planeta Marte, cuyo ciclo sinódico es de 780 días, empleando nuevamente el Tzolkin:
82 x 260 días = 780 x 27⅓ días = 27⅓ x 780 días
82 Tzolkines = 780 ciclos siderales de luna = 27⅓ ciclos sinódicos de Marte.
Aquí tenemos el mismo juego de reflejo que ya hemos observado con los ciclos de mercurio en 28 años solares: A través de 82 Tzolkines se refleja la luna sideral en el Marte sinódico.
Conclusión
Los mantos paracas expresan el arte de diseñar, geometrizar y “dibujar” números y ciclos astronómicos, lo cual nos abre un camino fascinante hacia una metodología matemática altamente creativa. Este arte de transmitir un conocimiento tan abstracto, que es el espacio-tiempo, logra un impacto visual impresionante. He realizado varios cálculos con la Yupana, que es “la calculadora Inca”, donde el cálculo es puro movimiento, y el resultado se muestra por una visibilidad tangible. He logrado aplicar en la Yupana las tablas arriba dibujadas, y me quedé fascinada con la idea de fijar los resultados a través de un arte visual. El método de emplear factores de multiplicación en la numerología, permite guiar al observador del Textil a ciclos más complejos, mostrando sus relaciones e interacciones. El textil se vuelve versátil, y depende de la destreza de su observador, cuanto se logra descubrir y entender. Conduce a un juego de numerosas posibilidades, donde la regla fundamental es la precisión, lo congruente. Pueda que eso sea uno de los factores, porque estos textiles hasta hoy no fueron entendidos, por la carencia del conocimiento astronómico en las careras universitarias relacionadas con la arqueología y el arte. También propongo no llamar a estos textiles “mantos funerarios”. No me parece lógico, que estos mantos hayan sido fabricados para la momia, para su entierro. Más bien, pudieron haber sido mantos que la difunta/ el difunto tejía y bordaba en su vida, con los cuales se les han envuelto en su entierro. Si partimos de esta perspectiva, estos mantos podrían informar mucho acerca del conocimiento y las habilidades de la persona momificada, de su estatus social y su especialidad.
Addendum:
Retomando el juego astronómico en los mantos de Paracas, tenemos aquí un textil más sencillo para decodificar (Fig. 11). En este manto se puede observar una corrección muy interesante: Cada par intercalado de flecos anaranjados fue removido, es decir, cortado posteriormente. Primero pensé que son flecos dañados, pero completando estos flecos faltantes (Fig. 12), resulta una regularidad exacta, lo que un daño por envejecimiento es imposible. Tomando en cuenta esta corrección, se llega al número de la Venus sideral:

Fig. 11: Manto Paracas Necrópolis. Paño central, algodón llano. Bordes de lana. Técnica: Bordado y anillado, 257 x 147 cms (Lavalle et Lang, 1990: 72)

Fig. 12: El manto con las aplicaciones de “reparación”.
Los flecos negros están agrupados a 10 unidades, segmentados por los flecos anaranjados. Los flecos negros dañados he redibujado con azul, y los flecos anaranjados cortados he completado con amarillo claro, pero estos no hay que contar, ya que fueron removidos (Fig. 11 y 12)
Solución propuesta:
Flecos: 20 grupos a 10 flecos negros más 5 flecos negros, y 10 pares de flecos amarillos
20 x 10 +5 = 205 flecos negros y 10 x 2 = 20 flecos amarillos
La suma es: 205 +20 = 225 flecos en total
225 días forman el ciclo sideral de Venus.
Contamos las figuras en el borde: 8 + 8 = 16
La Venus es visible durante 8 meses, desaparece, y reaparece otra vez por 8 meses. Es bonito observar este textil también bajo este aspecto, siguiendo al “movimiento” de las figuras. También, cada 8 años Venus está en el mismo punto de la eclíptica, culminando el ciclo pentagonal.
Si remplazamos cada figura antropomorfa con los ciclos siderales y sinódicos de la Venus, nos da las siguientes posibilidades:
16 x 225 días = 3600 días = 10 Tun
16 x 585 días = 9360 días = 1/10 Ahau = 1/ 100 del Gran Ciclo (= 5 Cuentas Largas)
La cabeza de la figura tiene 10 “serpientes”. Tomando eso en cuenta obtenemos:
10 x 16 x 585 = 93 600 = 1 Ahau
En este manto tenemos una hermosa visualización de la Venus, sus ciclos y su relación con el ciclo Ahau.

Fig. 13: Detalle. Se observa bien los flecos anaranjados cortados/ removidos para aplicar la corrección. Imagen de Lavalle et Lang, 1990: 73
Agradezco al Museo Chileno de Arte Precolombinopor haberme facilitado las fotografías originales de las piezas textiles de la exposición Paracas, lo cual me posibilitó realizar esta investigación, tomando en cuenta los detalles, que no son visibles en las publicaciones bibliográficas.
Un especial agradecimiento a Marcela Enriquez, ella entendió mi inquietud y fascinación hacia los mantos de Paracas y me permitió el acceso a los imágenes originales.
Bibliography
- Burns, W. 2010. El mundo de los Amautas, Universidad Alas Peruanas, Lima.
- Gonҫalez Holguin, D. 1952 (1608). Vocabulario de la lengua general de todo el Peru llamada lengua Qqicchua o del Inca, Universidad Nacional Mayor de San Marcos, Lima
- Lavalle, J. & Lang, W. 1990. Paracas, Banco de crédito del Peru
- Museo Chileno de Arte Precolombino, 2015, Mantos Funerarios de Paracas: Ofrendas para la vida
- Pinasco Carella, A. 2013. Punchaucancha, Templo Inca del Sol, Instituto Arqueo Arquitectura Andina (IAAA), https://arqueoarquitecturaandina.wordpress.com/2013/06/16/contemporaneidad-del-diseno-ancestral-punchaucancha/
- Rivas, P. 2017. Planeta(rio) Tierra, https://planetariotierra.blogspot.com/
- Zuidema, T. 2015. Códigos de Tiempo, Espacios rituales en el mundo andino, Apus Graph Ediciones, Lima